حل تفصيلي للسؤال الثالث من الأسئلة الوزارية - إثبات تشابه مثلثين للصف الصف العاشر العام في مادة الرياضيات – الفصل الثاني

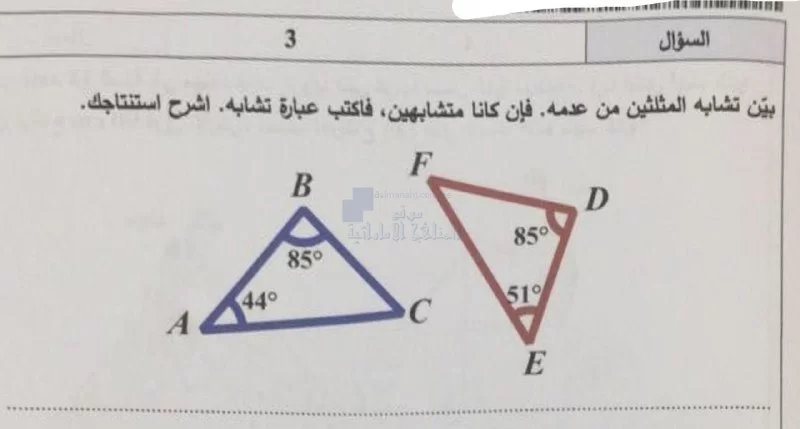توضيح المعطيات:

لدينا مثلثين، المثلث الأول \( ABC \) والمثلث الثاني \( DEF \)، وزواياهما كما يلي:

• \( \angle A = 44^\circ \) و\( \angle B = 85^\circ \) في المثلث \( ABC \).


• \( \angle D = 85^\circ \) و\( \angle E = 51^\circ \) في المثلث \( DEF \).

حساب الزاوية المتبقية في كل مثلث:

باستخدام مجموع زوايا المثلث:

\[
\angle C = 180^\circ - (85^\circ + 44^\circ) = 51^\circ
\]
\[
\angle F = 180^\circ - (85^\circ + 51^\circ) = 44^\circ
\]

الاستنتاج:

بما أن جميع الزوايا في المثلث الأول تطابق الزوايا في المثلث الثاني، فإن:

\[
\triangle ABC \sim \triangle DEF
\]

سبب التشابه:

• \( \angle A = \angle F = 44^\circ \).


• \( \angle B = \angle D = 85^\circ \).


• \( \angle C = \angle E = 51^\circ \).

وبذلك فإن المثلثين متشابهان حسب **حالة تطابق زاويتين (AA Similarity Theorem).**